Probablemente quieras ponerte tus gafas escépticas y configurarlas al máximo para esta. Un matemático italiano ha ideado algunas fórmulas complejas que pueden, con notable similitud, imitar las curvas de rotación de las galaxias espirales sin la necesidad de materia oscura.
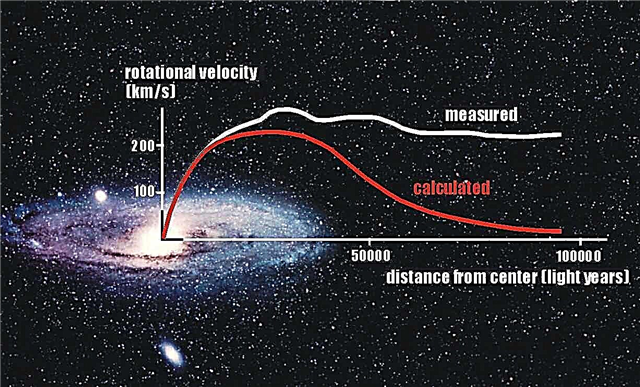
Actualmente, estas curvas de rotación galáctica representan evidencia clave de la existencia de materia oscura, ya que las estrellas externas de las galaxias giratorias a menudo se mueven alrededor de un disco galáctico tan rápido que deberían volar hacia el espacio intergaláctico, a menos que haya una masa presente 'invisible' adicional en la galaxia para mantenerlos gravitacionalmente en sus órbitas.
El problema se puede apreciar considerando el movimiento kepleriano de los planetas en nuestro Sistema Solar. Mercurio orbita al Sol a una velocidad orbital de 48 kilómetros por segundo, mientras que Neptuno orbita al Sol a una velocidad orbital de 5 kilómetros por segundo. En el Sistema Solar, la proximidad de un planeta a la masa sustancial del Sol es una función de su velocidad orbital. Entonces, hipotéticamente, si la masa del Sol se redujera de alguna manera, la velocidad orbital existente de Neptuno la movería hacia afuera de su órbita actual, lo que podría arrojarla al espacio interestelar si el cambio fuera lo suficientemente significativo.
La física de la Galaxia de la Vía Láctea es diferente del Sistema Solar, ya que su masa se distribuye de manera más uniforme a través del disco galáctico, en lugar de que el 99% de su masa se concentre centralmente, tal como está en el Sistema Solar.
No obstante, como explica este artículo anterior de la revista Space, si asumimos una relación similar entre la masa acumulativa de la Vía Láctea y la velocidad orbital de sus estrellas externas, debemos reconocer que los objetos visibles dentro de la Vía Láctea solo tienen un 10-20% de la masa que se requiere para contener la velocidad orbital de las estrellas en su disco externo. Entonces concluimos que el resto de esa masa galáctica debe ser materia oscura (invisible).
Esta es la visión de consenso contemporánea de cómo funcionan las galaxias, y un componente clave del modelo estándar actual de la cosmología del universo. Pero Carati ha llegado con una idea aparentemente inverosímil de que las curvas de rotación de las galaxias espirales podrían explicarse por la influencia gravitacional de la materia lejana, sin necesidad de recurrir a la materia oscura.

Conceptualmente, la idea tiene poco sentido. Posicionar una masa gravitacionalmente significativa fuera de la órbita de las estrellas podría atraerlas a órbitas más amplias, pero es difícil ver por qué esto se sumaría a su velocidad orbital. Dibujar un objeto en una órbita más ancha debería hacer que tarde más en orbitar la galaxia, ya que tendrá más circunferencia que cubrir. Lo que generalmente vemos en las galaxias espirales es que las estrellas exteriores orbitan alrededor de la galaxia en el mismo período de tiempo que las estrellas más internas.
Pero aunque el mecanismo propuesto parece un poco inverosímil, lo notable de la afirmación de Carati es que las matemáticas aparentemente entregan curvas de rotación galáctica que se ajustan estrechamente a los valores observados de al menos cuatro galaxias conocidas. De hecho, las matemáticas ofrecen un ajuste extraordinariamente cercano.
Con las gafas escépticas firmemente en su lugar, las siguientes conclusiones podrían extraerse de este hallazgo:
• Hay tantas galaxias por ahí que no es difícil encontrar cuatro galaxias que se ajusten a las matemáticas;
• Las matemáticas se han ajustado para que coincidan con los datos ya observados;
• Las matemáticas simplemente no funcionan; o
• Si bien la interpretación del autor de los datos puede estar en discusión, las matemáticas realmente funcionan.
La matemática se basa en los principios establecidos en las ecuaciones de campo de Einstein, lo cual es problemático ya que las ecuaciones de campo se basan en el principio cosmológico, que supone que el efecto de la materia lejana es insignificante, o al menos que iguala a gran escala.
Sorprendentemente, el artículo de Carati también señala otros dos ejemplos en los que las matemáticas también pueden adaptarse a las galaxias con velocidades de rotación decrecientes en sus estrellas exteriores. Esto se logra cambiando el signo de uno de los componentes de la fórmula (que puede ser + o -). Por lo tanto, por un lado, el efecto de la materia lejana es inducir una presión positiva que contiene la rotación rápida de las estrellas, evitando que salgan volando, y por otro lado, puede inducir una presión negativa para alentar una desintegración atípica en un curva de rotación de la galaxia.
Como dice el dicho, si algo parece demasiado bueno para ser verdad, probablemente no lo sea. Todos los comentarios son bienvenidos.
Otras lecturas:
Carati Efectos gravitacionales de la materia lejana en las curvas de rotación de las galaxias espirales.